Atomic Form Factor and Crystal Structure Factor
Here we consider X-ray diffraction intensity in terms of atomic form factor and crystal structure factor.
Thomson Scattering: X-ray Scattering by an Electron
The main source of X-ray scattering is electrons.
Classical Picture
First we use the free-electron approximation by ignoring the energy structure of electrons.
The motion of an electron in an oscillating electric field Eω, the resulting electric polarization is expressed as
pi=−e2Eω/mω2.
The oscillating polarization gives rise to radiation.
This is called Thomson scattering.
While the orbital and spin angular momenta of an electron also contributes to x-ray scattering,
it is smaller than Thomson scattering by a factor
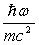 ,
which can be neglected in most cases.
,
which can be neglected in most cases.
Quantum Picture
The incident and the scattered x-rays can be represented by the vector potential A.
Here we use Coulomb gauge.
Thomson scattering corresponds to the first-order perturbation of 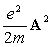 .
This perturbation dominates the x-ray scattering in most cases.
It is of note that this scattering term depends only on the electron density distribution, but not
on the energy state of an electron.
.
This perturbation dominates the x-ray scattering in most cases.
It is of note that this scattering term depends only on the electron density distribution, but not
on the energy state of an electron.
Real x-ray scattering is dependent on the energy state of each electron more or less, which is caused by other perturbation terms.
Atomic Form Factor
The amplitude of x-ray scattering by an atom is called atomic form factor.
Consider x-ray scattering by an atom.
Each electron of the atom contributes to the x-ray scattering.
When the scattering angle 2θ is zero, no phase shift appears wherever the x-ray is scattered.
When 2θ is not 0, however, some phase shift appears.
This phase factor Δφ depends on the position r, where the x-ray is scattered, and the wave vectors of the incident and scattered x-rays, as
Δφ=(ki−ks)r.
The amplitude of x-ray scattered at r is proportional to the electron density ρ(r) at r.
Therefore, the amplitude of x-ray scattering by an atom is represented as
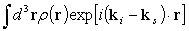 .
.
This is called the atomic form factor.
The atomic form factor of an isolated ion is defined in the same way.
In most cases, the electron distribution around an atom or ion is approximated to have the spherical symmetry.
Under this approximation, the atomic form factor is a fuction of the absolute value of ki−ks.
The atomic form factors f(sinθ/λ) for all the atoms and typical ions are listed in the International Tables for Crystallography A.
Crystal Structure Factor
The amplitude of x-ray scattering by a unit cell of a crystal is called crystal structure factor.
The spatial distribution of electrons in a unit cell is usually well approximated by the simple sum of the electrons of isolated atoms or ions.
We can hence simply add the atomic form factors of all the atoms located at
ri=xia+yib+zic
in the unit cell by taking the phase shifts into account.
Then we obtain
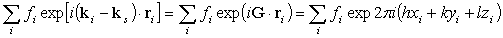 .
.
The sum is taken for a unit cell.
This is called the crystal structure factor F(hkl).
Here, we consider the Bragg condition: The scattering vector ki−ks is identical to a reciprocal lattice vector
G=ha*+kb*+lc*.
Calculation of Crystal Structure Factor
The crystal structure factor F(hkl) for hkl reflection of a crystal is calculated as follows.
- Find reciprocal lattice vectors a*, b*, c*.
- Calculate the absolute value of the scattering vector ha*+kb*+lc* and divide it by 4π to obtain sinθ/λ.
- Find the form factors fi(sinθ/λ) of all the atoms and ions constituting a unit cell.
- Calculate the phase factors 2π(hxi+kyi+lzi) for all the atom sites.
- Add fi(sinθ/λ) exp[2πi(hxi+kyi+lzi)] for all the atoms and ions in a unit cell.
Home
Taka-hisa Arima
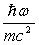 ,
which can be neglected in most cases.
,
which can be neglected in most cases.
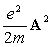 .
This perturbation dominates the x-ray scattering in most cases.
It is of note that this scattering term depends only on the electron density distribution, but not
on the energy state of an electron.
.
This perturbation dominates the x-ray scattering in most cases.
It is of note that this scattering term depends only on the electron density distribution, but not
on the energy state of an electron.
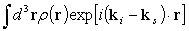 .
.
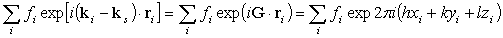 .
.