pi=−e2Eω/mω2
のように書ける。これによる放射を考えたものをトムソン散乱と呼ぶ。電子スピンや電子の軌道運動もX線の散乱源となるが、電気分極による放射よりもおおむね
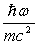 の因子だけ小さく、通常のX線回折では無視できる。
の因子だけ小さく、通常のX線回折では無視できる。
第0近似では、電子のエネルギー構造を無視して、自由電子とみなす。
その振動電場Eω中での電子の運動を考えると、生じる電気分極は
pi=−e2Eω/mω2
のように書ける。これによる放射を考えたものをトムソン散乱と呼ぶ。電子スピンや電子の軌道運動もX線の散乱源となるが、電気分極による放射よりもおおむね
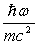 の因子だけ小さく、通常のX線回折では無視できる。
の因子だけ小さく、通常のX線回折では無視できる。
入射X線および散乱X線は、ベクトルポテンシャルAで表すことができる。
ここで、クーロンゲージを使うと、X線を表すスカラーポテンシャルは不要となる。
ベクトルポテンシャルに伴う電子の運動に関する摂動のうち
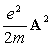 の一次摂動を考えたものが、上記のトムソン散乱となる。
の一次摂動を考えたものが、上記のトムソン散乱となる。
この摂動には、電子の個性が現れない。
すなわち、この効果による散乱振幅は電子密度分布にのみ依存する。
1つの原子によるX線の散乱振幅を原子形状因子と呼ぶ。
X線が1つの原子に入射したときの散乱を考えよう。
原子を構成する一つ一つの電子がX線の散乱に寄与する。
ここで、散乱角2θが0のときは、どの位置にある電子で散乱されても位相差はつかないが、2θが0でなくなると、散乱場所に依存した位相差がつく。
この位相因子Δφは、X線が散乱される場所rと、入射X線および散乱X線の波数ベクトルに依存し、次のようにかける。
Δφ=(ki−ks)r.
場所rで散乱される波の振幅は、rにおける電子密度ρ(r)に比例する。
以上のことを加味すると、原子1個によるX線の散乱の振幅は
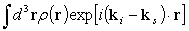
に比例する。これを原子形状因子と呼ぶ。
孤立したイオンについても、同じ式で原子形状因子を定義する。
多くの場合は、原子やイオンの周囲の電子分布を球対称と近似してもあまり問題はない。
この近似の下では、
原子形状因子は、ki−ksの絶対値のみの関数となる。
X線散乱の値はInternational Tables for Crystallography Afにsinθ/λの関数として掲載されている。
1つの単位胞によるX線回折の振幅を結晶構造因子と呼ぶ。
単位胞内の電子の分布については、通常、単位胞内のそれぞれの原子あるいはイオンが孤立しているとするのが良い近似となる。そこで、X線の回折源についても、全部の原子やイオンの電子分布を単純に足し合わせたものとみなすのが良い近似となる。
単位胞の中の
i番目の原子がri=
xia+yib+zicにあるとき、単位胞内の全ての原子によるX線の回折の振幅を足せばよい。
具体的には、
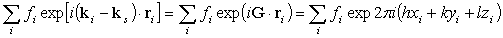
上記の和は単位胞について取る。
ここで、結晶によるX線回折は、散乱ベクトルki−ksが
逆格子空間の格子点G=
ha*+kb*+lc*
に一致しなくてはならないというブラッグの条件を用いた。
上式を結晶構造因子と呼び、F(hkl)などと書く。
上記より、 ある結晶のhkl反射についての結晶構造因子は次のように計算すればよい。
物質系専攻 有馬孝尚